A seal has the primary function of limiting leakage caused by a pressure difference. The leakage flow rate is governed by microscopic channels that exist at the interface between two rough surfaces. As the contact pressure increases, the available flow path narrows, which in turn increases the flow resistance.

At a certain point, no channels remain that form a continuous connection between the high-pressure and low-pressure sides of the seal. This point is referred to as the percolation threshold. In cases where surface roughness is isotropic and normally distributed, this threshold occurs when approximately 42% of the nominal surface area is in actual contact (i.e., the asperity peaks are touching) [2].

‍

Relevant Scales

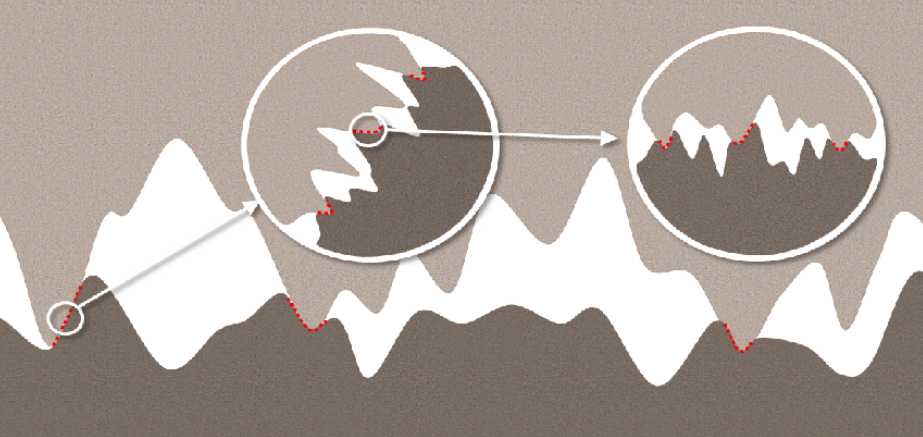
A key question is: at what scale should this contact be evaluated? At low magnification, the entire interface may appear to be in contact. However, when zooming in, only the roughness peaks clearly touch. At an even finer scale, new roughness features become visible, showing that true contact still occurs only at a fraction of the apparent contact area. The deeper we zoom, the smaller the ratio between the true and nominal contact areas becomes.

The appropriate scale for evaluating leakage depends on the application:

• ‍Biological sealing: If preventing bacterial transport is the main concern, a micrometer scale is sufficient (since a bacterium is typically around 1 μm in size). ‍
• Fluid sealing: If liquid or gas leakage is the concern, the molecular scale (on the order of ~1 nanometer) becomes relevant.

For a seal to be considered leak-tight to fluids, the ratio of the true contact area to the nominal contact area must exceed 42% at the nanometer scale. The nominal interface pressure required to achieve this under vacuum conditions is called the percolation pressure. This is a characteristic property of the interface, and it can be determined experimentally or by simulation-based modeling when the surface roughness and mechanical properties of the interface materials are known.

‍

‍

Modeling Sealing Behavior

When the fluid pressure is negligible compared to the nominal contact pressure, it can be ignored in the model. Under this assumption, leakage performance can be assessed by calculating the contact pressure using a Finite Element Method (FEM) model and comparing it to the percolation pressure.

If, however, the fluid pressure is of the same order of magnitude as the contact pressure, it cannot be ignored. Fluid pressure contributes to additional deformation of the seal, which alters the contact pressure. Conversely, the contact pressure influences the fluid pressure distribution within the contact zone—making this a coupled problem.

At Reden, we developed a coupled simulation method within ABAQUS to address this interaction. Some figures follow, of which the interpretation is given below:

‍

‍

• On the non-contact side (left in the figure), the surface pressure equals the fluid pressure.
• As contact begins, surface pressure rises due to the combined effect of fluid pressure and structural contact pressure.
• The effective contact pressure is defined as the difference between the total surface pressure and the fluid pressure. In vacuum conditions, this corresponds to the pressure needed to produce the same deformation of the rough surface.

This effective contact pressure is then used to evaluate flow resistance:

• When it exceeds the percolation pressure, flow resistance rises sharply, leading to a “kink” in the pressure profile.
• When it falls below the percolation pressure, flow resistance drops rapidly, and the fluid pressure aligns with the external pressure outside the seal.

Additionally, the effective contact pressure can be used to estimate friction forces at the interface. If the percolation pressure is not exceeded, the method can also be used to calculate the leakage flow rate directly.

This modeling approach is applicable in 3D, 2D, and axisymmetric configurations, making it widely useful for engineering design and simulation of sealing interfaces.

‍

[1] Pérez-Ràfols F. Two-Scale Stochastic Modelling and Analysis of Leakage Through Metal-To-Metal Seals. Luleå University of Technology, 2018.

[2]  Dapp, W.B., Lücke, A., Persson, B.N.J., Müser, M.H.: Self-affine elastic contacts: percolation and leakage. Phys. Rev. Lett. 108, 244301 (2012)

‍