A video on Youtube [1], with a link to a recent paper “Exotic mechanical properties enabled by countersnapping instabilities” [2] has intrigued some of us at Reden, and many others. The video, published by AMOLF, makes a heroic claim based on the fact that a cup of water, suspended by the ‘exotic mechanism’ rises as some water is added to it. Though this is indeed counter-intuitive, the paper does not make very clear why this effect is ‘one giant leap for mechanics’, though several applications are given.
The paper explains in detail how the mechanism works, but the explanation is not clear enough for Reden Makes Sense. Luckily, a clearer example of the same behaviour can be devised, with help of Wikipedia: the Braess' paradox [3]. There is a close link with this strange phenomenon, this time in traffic. In certain cases, the travel times get shorter if a busy road is... closed. But first, we’ll look at the springs.
The AMOLF mechanism appears to be an implementation of the spring paradox [4]. In the spring paradox, a weight is supported by two springs (picture on the left). The springs are connected by a short length of rope (red). When the red rope is cut, the weight is lifted, contrary to what one would expect! The AMOLF mechanism is a reversible version of this example; it snaps back to the original state if the force on it is removed.
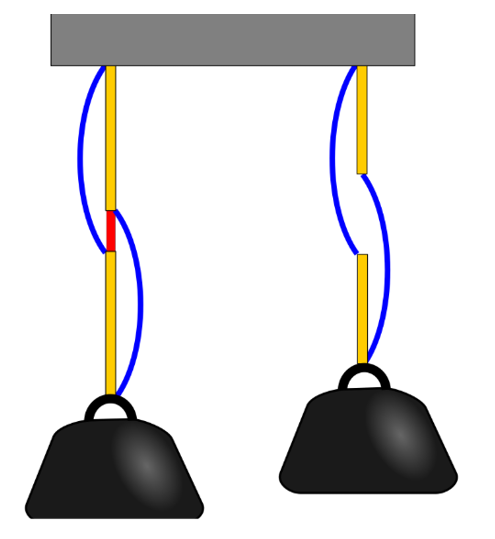
Can we make sense of this?
The video and Wikipedia explain that cutting the rope switches the mechanism from ‘two springs in series’ to ‘two springs in parallel’, which is supposed to explain why the weight is lifted upon cutting of the red rope. But what happens to the spring energy and the potential energy of the weight? And where does the energy come from which is necessary to lift the weight?
It is time for some numbers, and also for a clearer picture.
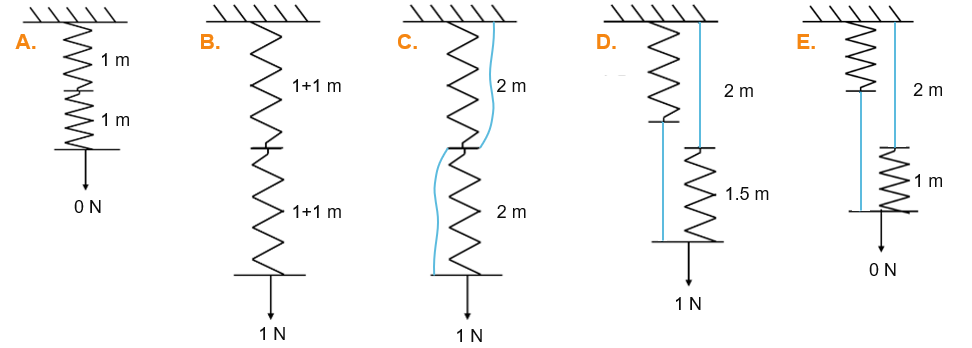
For easy calculation, we use springs with an initial length of 1 m, a stiffness of 1 N/m, and a force of 1 N.
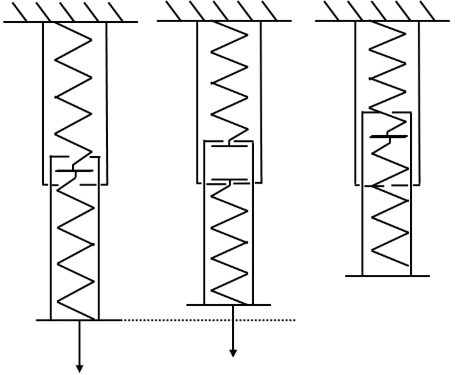
As long as the two springs are connected by the short string, the two springs and the long ropes carry no weight, it is clear that each spring is extended by 1 m (the full force works on both springs), and the weight hangs 4 m below the attachment point (we assume the short string is so short it doesn't add to the total length). This situation is illustrated as situation B in the schematic below.
In preparation for cutting the connection between the springs, the long ropes are attached (just without carrying any weight, but also without slack), for which they need to be 2 m long. Cutting the rope connecting the springs causes the long ropes to become load bearing. Each spring and long rope pair now carries half the weight. The springs contract to 1+0.5 =1.5 m (from 1+1 m). The weight thus comes to rest at 2 (rope) + 1.5 (spring) = 3.5 m.
It is important to realise that, when the force is removed, the configuration with the two ropes and no connection between the springs contracts to 3 m, whereas the original configuration contracts to 2 m. This indicates that cutting the short connecting rope is an action which cannot be undone without putting in effort.
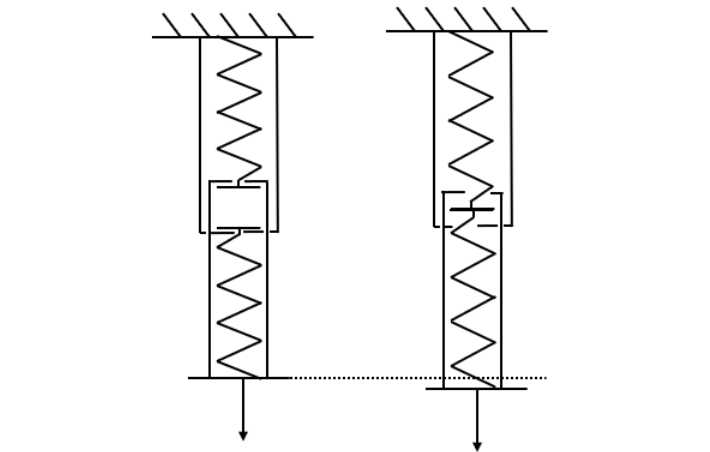
Bracket analogy
Another way of explaning this behaviour is by imagining brackets instead of strings.
We start with the situation with the springs detached from each other. They both pull on a bracket and share the load. If we want to bring the springs into contact while they are loaded, we have to pull on both, which makes them longer, and costs energy. The brackets are now not contributing anymore, and both springs carry the full weight.
Braess' paradox
Now the example of roads. The paradox of Dietrich Braess (a German mathematician) was illustrated in a 1968 paper by him by a traffic situation [5].
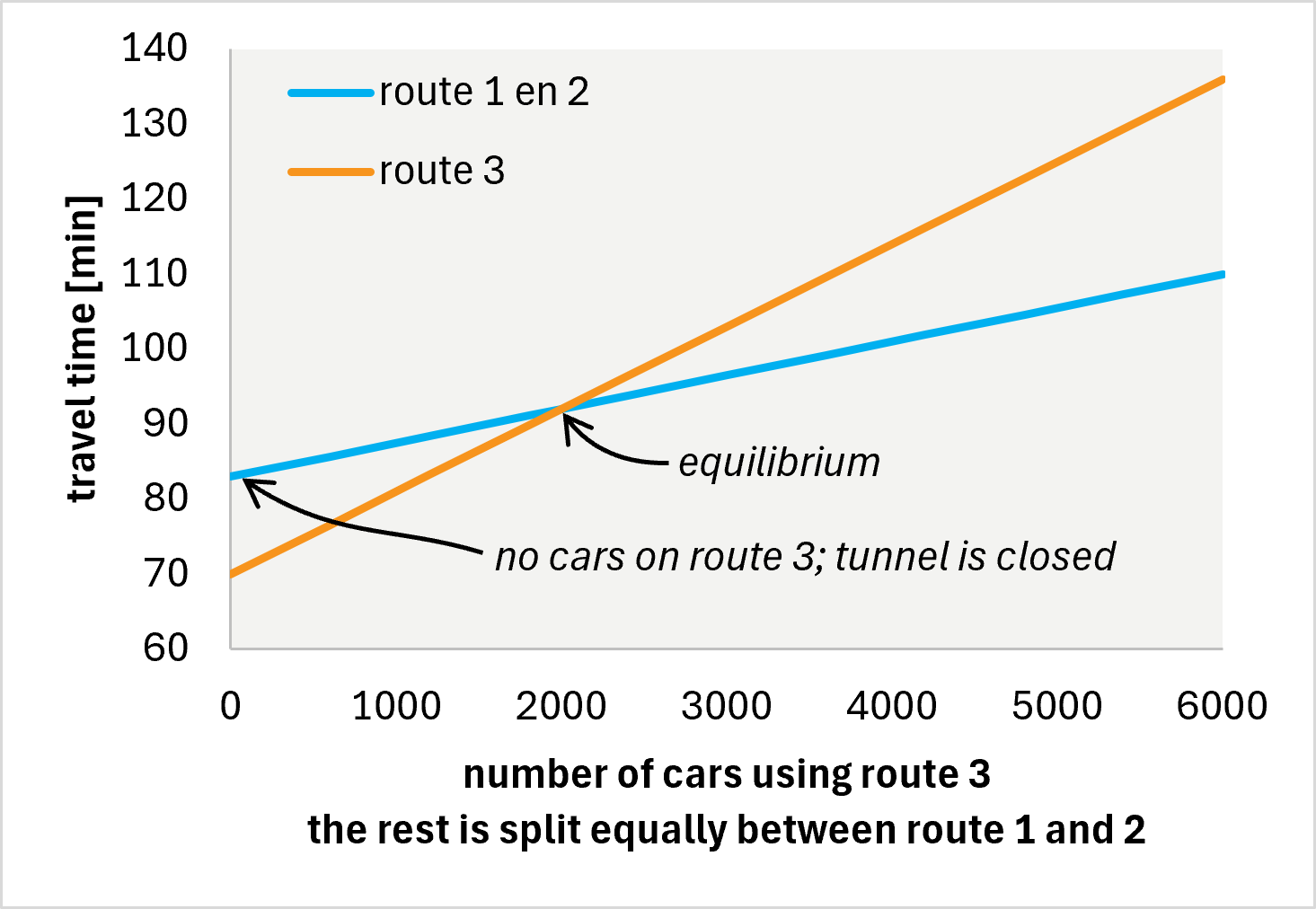
There are four cities and five roads. The local roads (orange) are short and a bit cramped, so the travel time depends largely on the amount of traffic x (number of cars per hour divided by 1000): t = 10*x. The highways (blue), on the other hand, are spacious, but a lot longer. The travel time on them is t = 50 + x (travel times in minutes). There is also a tunnel through the mountain between city B and city C, in which the travel time is t = 10 + x. There are 6000 drivers per hour who want to go from A to D (i.e. xtotal = 6) and have a choice between three routes:
- Taking the autobahn to C and then the landstraße to D.
- Taking the landstraße to B and then the autobahn to D.
- Taking both landstraßes and the tunnel.
It is assumed the tunnel is one way, eliminating a fourth option in which both autobahns would be utilized. Although this only makes the analysis easier; it does not change the outcome.
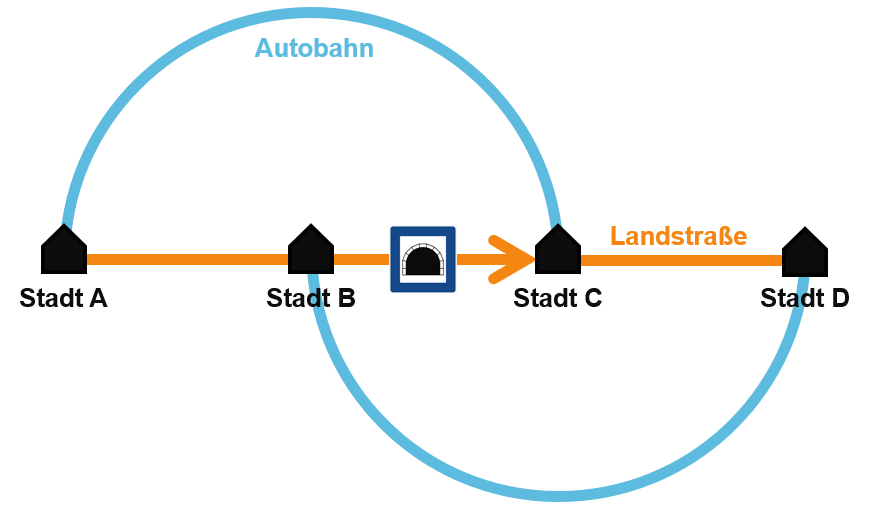
The equilibrium solution is that 2000 take each route, and all need 92 minutes to reach D6.
Now, if the tunnel is closed, route 3 is not possible anymore. It turns out that in that case the new equilibrium (3000 on both remaining routes) leads to a travel time of 83 minutes, which is 9 minutes faster! In other words, opening the tunnel delays the travel time for all drivers!
You may have seen how this situation is analogous to the spring paradox. The tunnel is as the connection between the springs. If it is cut/closed, both routes operate in parallel, and share the ‘load’, but with the tunnel in place, there is a serial connection. In particular, both local roads carry more load.
Back to the springs
The magic of the video is largely dispelled by the discovery that the system in the video, with the fancy 3D printed parts, is, in fact, an automatic version of the springs and strings. It switches between the two states of high and low stiffness. If we introduce an automatic coupling between the two springs, which releases if a certain force is exceeded, this then switches from A to B. By pushing the bottom end up to situation C, the coupling is engaged again.
Whether or not this is a ‘giant leap for mechanics’ depends on the applications. The behaviour may be used to avoid oscillations in constructions by passively switching between two resonance frequencies, as explained in the recent Veritasium video on this subject [6]. As in all paradoxes, it appears to be opposed, in this case to physics. But if you look more closely, it is not really against normal physics. In the case of the spring paradox, the only reason the weight can go up when you cut the string is that energy is released which was first put into it (either by you or by gravity). If you look carefully, there is no mystery.
The spring paradox is a very intriguing and entertaining application of simple mechanics. Now it is for inventors to come up with a useful application. And, if you need help in bringing such application to maturity and then to the market, why not engage the Reden Jumpstart?
[1] These structures shrink when pulled: Counter-snapping instabilities
[2] Exotic mechanical properties enabled by countersnapping instabilities
[3] Braess's paradox - Wikipedia
[5] paradox.pdf “Über ein Paradoxon aus der Verkehrsplanung”




