Introduction
Since the dawn of time, mankind knows that a sling is useful for throwing stones. David uses a sling to kill Goliath, and the medieval onager (see figure) uses the same principle of launching an object at high speed using a rotating link.

SpinLaunch takes this ancient idea into the space age by proposing to sling satellites into orbit. Kinetic energy in the form of velocity at launch does not have to be carried in the form of fuel. The big gain is that not carrying fuel means not having to accelerate the fuel. In a normal rocket, the mass of the fuel is much more than the payload, so most of the energy is spent on accelerating the fuel.
The SpinLaunch website promises to reduce drastically the energy required to bring satellites into orbit. It mentions the most important limitation, i.e. the fact that the enormous ‘g-forces’ mean the system is unsuitable for manned flights.
A first impression
The website does not dwell on the problems which must be solved before SpinLaunch can be used. There are at least five problems which would kill the idea unless they can be solved.
At Reden, we like to have numbers to base an impression on. A simple calculation can give more insight than a subjective impression. ‘Big’ or ‘fast’ has little meaning without a number.
Let’s first look at the speed of the missile at launch and the energy involved.
Speed
To launch an object into orbit, you have to accelerate it to roughly 30,000 km/h (this is for a height of 1500 km (Low Earth Orbit)). SpinLaunch plans to launch small rockets, encased in container, at 8000 km/h (2222 m/s). This is not enough, so a small rocket is included in the package, comparable to the second stage of a normal rocket, which accelerates the payload another 22,000 km/h. This rocket produces all its emissions in the outer atmosphere. SpinLaunch claims that its missile is launched with 85% less fuel, on board at launch, than a conventional rocket. This is possible because it is launched at high speed, with sufficient kinetic energy.
The rotating arm which gives the missile its velocity is roughly 45 m long, with a shorter counterweight arm on the other side. It has to rotate at ω = v/r = 2222(m/s)/45(m), or almost 50 rad/s.
Energy
The energy saving is possible because the fuel that is not carried does not have to be accelerated. To quantify this, let’s use the numbers for SpaceX’s Falcon 9 (numbers are taken from Wikipedia). Its first stage contains 146,020 litres of Rocket Propellant-1 (basically kerosene, with a lower combustion value 43.0 MJ/kg). This is oxidised using 245,620 litres of liquid oxygen. The oxygen requires roughly 2 kWh/Nm, according to Weber et al. [1] Using a density of kerosene of 0.8 kg/l, and a volume ratio of 0.8 Nm/l, there is 5023 GJ of energy in the kerosene, and 1415 GJ was needed to supply the liquid oxygen. In total, this is 6438 GJ. The payload to Low Earth Orbit is 22,800 kg, so the energy use per kg for the first stage is 282 MJ.
The energy needed for SpinLaunch is: energy to pump air out of the big chamber, the energy to spin the rotor and the energy to accelerate the missile.
The energy to achieve vacuum in the chamber is of the order of 1500 MJ (100 m diameter, 1 m high on average (estimated, no data available), 1 bar, efficiency 50%). The energy to speed up the rotor is of the order of 16000 MJ (but can, in principle, be recovered. Assumptions: arm length 2 x 45m, weight 12500 kg, rotation 50 rad/s). The missile has a kinetic energy of 0.5 * 200 kg * (2222 m/s)^2 = 494MJ.
If 50 % of the rotation energy of the arm is recovered, the energy input is approximately 10,000 MJ/ 200 kg = 50 MJ/kg. This is 80% less than for the Falcon 9.
We can conclude that SpinLaunch’ claim of energy saving is probably correct (they have the exact data, but we came close).
[1] Comparison of the Energetic Efficiency of Gas Separation Technologies Using the Physical Optimum by the Example of Oxygen Supply Options Samanta A. Weber, DirkVolta and Jürgen Kuck.
Problems
Now that we know the technique is interesting from an energy point of view, it is time to look at problems (and to quantify them). Without much thought, we can identify five problems:
- Centrifugal forces on the arm
- Rotation of the missile when released
- Timing of release
- Unbalance of rotor after release of the missile
- Safety
These problems can be quantified.
Centrifugal forces on the arm
Quite apart from the load imposed by the missile, the arm needs to be quite strong to withstand the centrifugal effect. The rotation is so fast, that many materials would disintegrate. What about the numbers?
For simplicity, we assume a constant cross-section for the arm. The stress in the arm is zero at the end and increases towards the centre, with a gradient of the local centrifugal acceleration times the density:
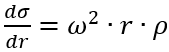
Integration leads to:
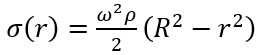
Where R is the radius of the arm and r the radial coordinate. The velocity at the tip is ω*R, so the following equation applies at r=0:
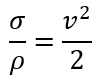
where σ is the normal stress in the arm, and ρ is the density of the material.
For carbon fibre, Wikipedia gives a value of σ_yield/ρ of 3911 kN/kg. The minimum value necessary is /2 = 2469 kN/kg. Thus, 64% of the available strength of the carbon is needed to support the arm itself. (This can be improved by changing the shape. However, the images of SpinLaunch suggest a simple shape).
There is an additional stress due to the missile. The yield strength of the carbon fibre is 7000 MPa, and 64% is needed to support itself, so there is roughly 36% of 7000 MPa left to deliver the force for the missile. If we assume 250 kg, the extra force is 25.7 MN. The minimum cross-section area of the arm is therefore 0.11 m, which could be, for instance, 5 by 22 cm. In practice, a larger and non-uniform cross-secion will be needed to supply a safety margin.
The first problem, therefore, seems surmountable.
Rotation of the missile when released
As long as the missile is attached to the rotor, it rotates too. The angular velocity is v/R, or 2222/45 = 50 rad/s or almost 8 revolutions per second, or 472 RPM.
In simple terms, for a rotation of 90°, the missile needs only 31 ms, in which it travels 71 m. In air, the missile might stabilise, but in the exit tube, in which there is a (partial) vacuum, and which looks to be around 40 m long, the rotation will be unhindered,and amount to 50° !!
This effect can be seen in the video of the suborbital test on the SpinLaunch-site. For this prototype, the numbers are different, with one full rotation corresponding to 75 m of flight. The frames with the enlargement of the missile show a 15° rotation in 90 m ( 140 – 230 m) of flight for the suborbital (roughly). This suggests that the problem was solved at least partially.
We found a way to solve this problem. It is simple in principle, but may prove difficult to realise. Can you think of a solution to this problem?
SpinLaunch mentions neither the problem nor the solution. Can their (partial) solution be scaled to the full size machine?
Timing of release
The release must be executed at the precise point that will send the missile through the launch tube. If we assume a tolerance of half a degree, the time slot is 0.17 ms. Electronically, that shouldn’t be a problem. The mechanical requirement is that the mechanism must exert a force of 25.7 MN (roughly 2500 tonnes, or 80 fully loaded 40 ft shipping containers) before release, and nothing 0.17 ms later. This seems a design problem with a solution, not an impossibility.
Unbalance of rotor after release
If the rotor is balanced with the missile attached, it will become suddenly and severely unbalanced upon release of the missile. The bearings will have to absorb the same force that was, until launch, taken up by the missile (the 80 fully loaded containers). The same applies to the rest of the structure, in particular the foundation. This force will have a continuously varying direction, initially changing direction 8 times per second. Without diving into bearing calculations, it seems that bearings can be found in heavy industrial applications which are up to this task. They will have to be substantial, as will the foundation.
Safety
The safety concern is closely related to all the above points. It is difficult to build a comfortable safety factor into the rotor design. If the rotor fails, the stored energy is released instantly. The structure of the enormous vacuum chamber must be very secure; if it folds inwards, the rotor with its very high speed will hit it. The design of the enormous housing, without internal supports, which can withstand a pressure of almost 1 bar is another area which we will leave for now, but it is certainly challenging.
By the way, can you see how vague the safety paragraph is without numbers?
Discussion
In a case with so many challenges, one unsolvable problem will stop the project. In this case, the problem of missile rotation should be addressed (if it has not been solved already). Of the other problems, the forces on the arm, the timing of release and the unbalance seemed daunting at first, but the first exercise to put numbers in has made them seem less problematic. The safety concern should be quantified too, but there seems no point if the installation does not shoot straight.




