The promise
In this time of high energy prices and low temperatures, the heat pump is more popular than ever. The high efficiency gas boiler is surpassed in efficiency by the heat pump. ‘Efficiency’ is replaced by another word to express its superior performance: COP, or Coefficient of Performance. For a heat pump a COP of 1 means an efficiency of 100% [1]. In practice, a heat pump can often achieve a COP of 4 or 5, although the performance drops if conditions are less favourable. A heat pump struggles when the source temperature is very low or the discharge temperature high.
Impressive as the heat pump’s performance may seem, it did not satisfy Fluid Mechanics Ltd engineer Michael Crowley. He has invented a new type of heat pump, the Near Isothermal Stirling Heat Pump (link). This invention, of which prototypes have been tested, achieves 60% of the theoretical maximum performance against current technology’s 40%. If this can be maintained for the production devices, it would reduce the energy consumption of a domestic heat pump by a third.
Is it possible to improve so drastically the performance in a mature technology sector? Conventional heat pumps use vapour compression technology which has been around for refrigerators and air conditioners for many years, after all.
At Reden, we like to see numbers to substantiate claims. Often, these are missing (see earlier columns in this series), but in this case, they are provided, which is very reassuring. Now we like to understand them.
[1] Efficiency here means the useful energy delivered divided by the (non-free) energy put in. The heat pump also gets heat from a heat source, but this is free, so it does not count as input energy. A better definition of efficiency, for any heating device, would be to compare the performance to the theoretical maximum. This will always be lower than 100%.
Understanding Heat Pumps
Heat pumps are magic machines with their miraculous performance, until you understand what they do. To explain this, we use a water analogy. In this analogy, water corresponds to heat, water height corresponds to temperature, water flow to heat transfer and water leaks to imperfect insulation.
A heated house in a cold environment looks like this:

If there is no heating, the water level (temperature) in the house will eventually be equal to that outside. Now, to top up the water level (temperature), there are two methods:
- The gas fired heater tops up from a high level (the gas flames are very hot).
- The heat pump pumps water from the level available outside to the level in the house [2]. It is becoming clear why this may cost less energy; the high level from which the water is poured in case of the heater is a waste of energy.
So, the reason that a heat pump is so efficient is that 1) it takes heat available at a low level for free, and 2) it does not raise this heat higher than necessary.
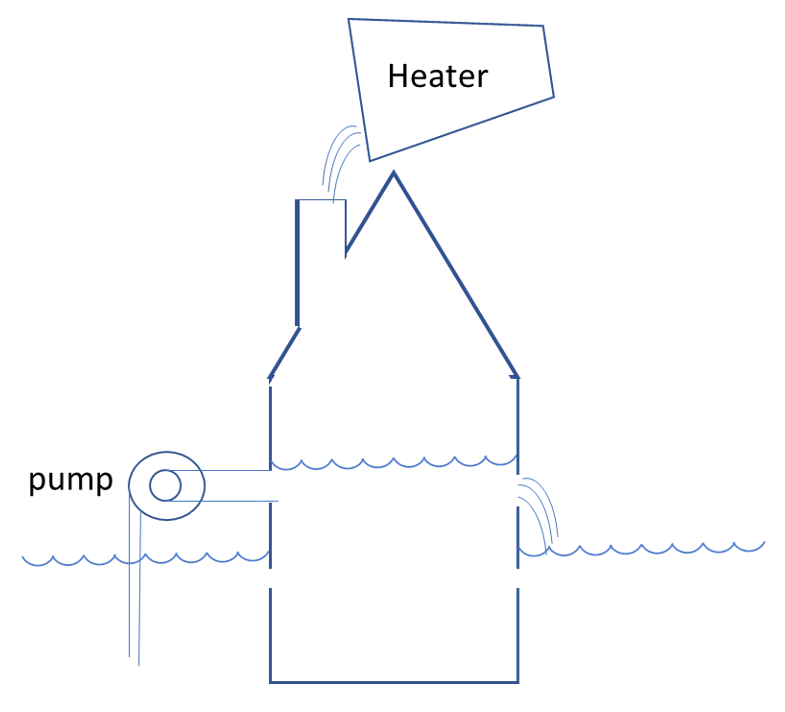
[2] For simplicity, we consider here an air source heat pump, so the outside temperature is the relevant level
Heat Pump Efficiency and the Stirling Engine
The Stirling engine is an old invention which has never really caught on despite the fact that it has many excellent qualities. One of these is the fact that it can achieve, in theory, the Carnot efficiency, which states how much useful work can be harvested from a heat difference. Another quality is that it can be used in reverse, for instance as a heat pump. This can be illustrated in the water analogy.
The heat engine’s analogon is a water mill (water flows from high to low and drives a water wheel). The heat pump analogon does the reverse, and if it is driven by the water mill, and everything works without losses, then it should be able to pump the water driving the water mill back to the same level.
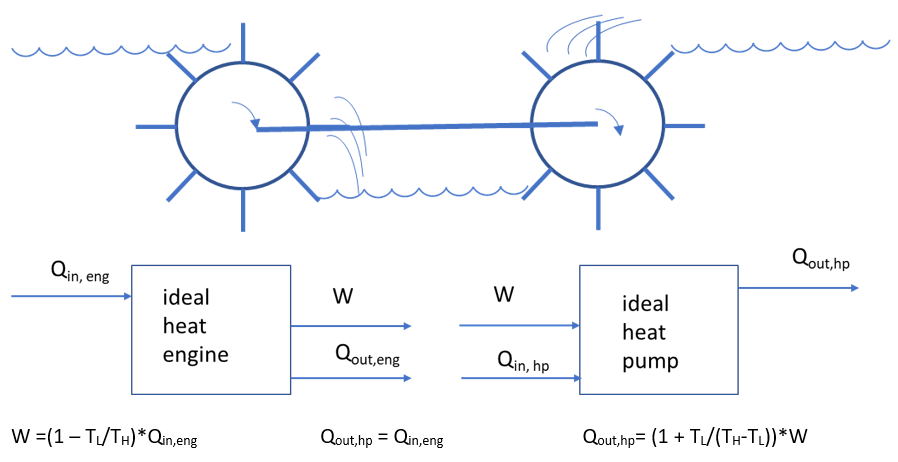
In the water analagon, it is clear that the water level after the pump can never be the same as before the water mill. For the discussion of the Near Isothermal Stirling Heat Pump, it is important to note that heat, like water, only flows when there is a gradient. The water has to flow into the water wheel (a level drop), and out of it (another level drop). It likewise has to flow into the pump wheel (loss) and from the wheel to the upper level. A heat pump has to deliver a greater temperature lift than simply the difference between the outside air and the temperature in the house.
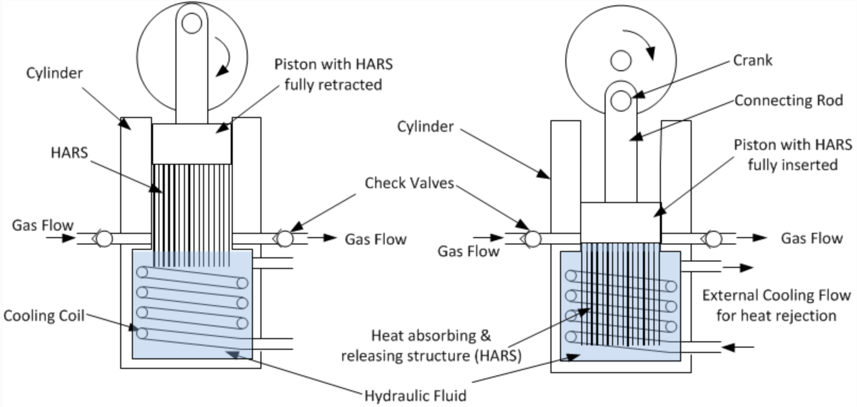
And this is the area on which Michael Crowley has focused. His heat pump is based on the Stirling cycle (gas is compressed, gives of heat at TH , is expanded, and takes up heat at TL). The core of the invention is the HARS (heat absorbing and releasing structure). This consists of a series of aluminium plates which are spaced close together. The gas, as it is being compressed, gives off heat to the plates, so that the gas temperature rises very little (hence the ‘near isothermal’). The plates exchange the heat with a fluid, again with a small temperature difference. Otherwise, the system works like a conventional Stirling cycle (see Stirling engine -Wikipedia).
The importance of the near isothermal operation becomes clear from the COP-equation. For TL= 7°C, TH = 35°C, the theoretical maximum COP is 11. If a machine has 25% mechanical and electrical losses and internal temperature drops of 3,5°C, then the COP is 6.67. This is 60 % of the theoretical maximum of 11, and this is what Fluid Mechanics Ltd claims. If the temperature drops in the machine were 7°C instead of 3,5°C, the performance would drop to a COP of 5.6, or a 16% deterioration! For 10°C internal drops, the COP would be 5.0. The internal temperature differences should, therefore, be as low as possible.
How does this novel heat pump compare with existing systems? I have found a Hitachi heat pump (their RWM-2.ONE air-to-water heat pump) with the following performance: COP 5.25 when the air is 7°C and the water leaving the system is 35°C. This is 47.7% of the theoretical maximum COP of 11 (1+280 K/28 K = 11).
Note that the Hitachi COP is lower than the COP for the near isothermal Stirling heat pump, but if the latter would not be nearly isothermal, it would probably perform worse than the Hitachi.
Finally, the systems can be compared in terms of primary energy, assuming the electricity driving the heat pumps was generated from fossil fuels with an efficiency (including transport) of 45%.
For 7°C/35°C (cold/hot temperature), the following COPs and overall efficiencies result. (assuming 45% overall efficiency of electricity generation, distrubution, conversion)
Conclusion
The near isothermal Stirling heat pump is based on a clever idea. This idea enables the construction of a more efficient heat pump for domestic heating. The device is not on the market yet, so final performance numbers are still a little uncertain, but the performance claimed has been demonstrated in prototypes, and can be explained from basic thermodynamics. It makes sense. Let’s hope the development to market introduction does not take long.



